Sannsynligheten regulerer våre liv: Bayes teorem

Sannsynligheten regulerer våre liv - vi bruker den hver dag uten å være klar over det. I denne artikkelen diskuterer vi en av dens viktigste teoremer: Bayes teorem.

Vurdert og godkjent av psykologen Sergio De Dios González.

Skrevet av Paula Villasante

Siste oppdatering: 27 desember, 2022

Bayes teorem er en av sannsynlighetens søyler. Teoremets navnebror kommer fra Thomas Bayes (1702 – 1761), som foreslo teorien i det attende århundre. Men hva var det forskeren forsøkte å forklare? Ifølge Meriam-Webster-ordboken er sannsynligheten “forholdet mellom antall utfall i et uttømmende sett med like sannsynlige utfall som gir en gitt begivenhet til det totale antall mulige utfall”.

Mange sannsynlighetsteorier styrer verden. For eksempel, når du går til legen, gir de deg resept på det som sannsynligvis vil kurere deg. I tillegg fokuserer annonsører sine kampanjer på folk som har større sannsynlighet for å kjøpe produktet de markedsfører. Videre velger du din daglige pendling på ruten som har størst sannsynlighet for å ta mindre tid.

Bayes teorem: Loven om total sannsynlighet

En av de mest kjente sannsynlighetslovene er loven av total sannsynlighet. Det er viktig å analysere hva loven om total sannsynlighet er. For å forstå det gir vi deg et eksempel.

La oss si at i et tilfeldig land er 39% av innbyggerne kvinner. Vi vet også at 22% av kvinnene og 14% av mennene ikke har en jobb. Så hva er sannsynligheten P at en person valgt tilfeldig fra den aktive befolkningen i dette landet er arbeidsløs P (U)?

I følge sannsynlighetsteorien er det slik vi vil uttrykke sannsynligheten:

• Sannsynligheten for at personen er en kvinne: P (W)
• Sannsynligheten for at personen er en mann: P (M)

Siden vi vet at 39% av innbyggerne er kvinner, så kan vi utlede at P (W) = 0,39

Dermed kan vi konkludere at P (M) = 1 – 0,39 = 0,61.

Også det oppgitte problemet gir oss betingede sannsynligheter:

• Sannsynligheten for at en kvinne er arbeidsløs: P (U | W) = 0,22
• Sannsynligheten for at en mann er arbeidsløs: P (U | M) = 0,14

Derfor, ved å bruke loven om total sannsynlighet, får vi:

P (U) = P (W) P (U | W) + P (M) P (U | M)

P (U) = 0,22 × 0,39 + 0,14 × 0,61

P (U) = 0,17

Sannsynligheten for at en valgt tilfeldig person ikke vil ha en jobb P (U) vil være 0,17. Du kan se at resultatet ligger mellom de to betingede sannsynlighetene (0,14 <0,17 <0,22).

Bayes teorem

Anta at du valgte en tilfeldig voksen til å fylle ut et skjema, og du skjønte at de ikke har en jobb. I så fall, og med hensyn til det forrige eksempelet, hva er sannsynligheten for at denne personen du valgte tilfeldigvis er en kvinne [P (W | U)]?

For å løse dette problemet må du bruke Bayes teorem. Spesifikt bruker du dette teoremet til å beregne sannsynligheten for en hendelse med tanke på tidligere informasjon du har om denne hendelsen. Du kan beregne sannsynligheten for hendelse A, og også vite at denne hendelsen A oppfyller visse egenskaper (B) som påvirker sannsynligheten.

I dette tilfellet snakker vi om sannsynligheten for at personen du valgte tilfeldig for å fylle ut et skjema er en kvinne. I tillegg vil imidlertid sannsynligheten ikke være avhengig av om personen har en jobb eller ikke.

Bayes teorem, metode

Som alle andre teoremer trenger vi en formel for å beregne sannsynligheten:

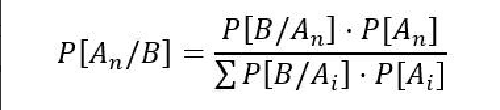
Selv om det virker vanskelig, har alt en forklaring:

• For å begynne, er B hendelsen vi har tidligere informasjon om.
• På den annen side refererer begrepet A (n) til de forskjellige betingede hendelsene.
• Vi har betinget sannsynlighet i telleren. Dette refererer til sannsynligheten for at noe (en hendelse A) vil oppstå, og vet at en annen hendelse (B) også oppstår. Vi definerer dette som P (A | B) og uttrykker det som “sannsynligheten for en gitt B”.
• I nevneren har vi like P (B).

Et eksempel

Gå tilbake til forrige eksempel. Anta at du valgte en tilfeldig voksen til å fylle ut et spørreskjemaet, og du innså at de ikke har en jobb. Hva er sannsynligheten for at denne personen er en kvinne [P (W | U)]?

Vel, med tanke på det forrige eksemplet, vet vi at 39% av den aktive befolkningen er kvinner. Vi vet da at resten er menn. I tillegg vet vi at andelen arbeidsløse kvinner er 22% og prosentandelen arbeidsledige menn er 14%.

Endelig vet vi at sannsynligheten for å velge en tilfeldig, arbeidsløs person er 0,17. Så, hvis vi bruker Bayes teorem vil resultatet vi får, være 0,5 sannsynlighet for at en person valgt tilfeldig, av alle de som er arbeidsløse, vil være en kvinne.

P (W | U) = (P (W) * P (U | W) / P (U)) = (0,22 * 0,39) / 0,17 = 0,5

Vi konkluderer denne artikkelen ved å referere til en av den mest hyppige forvirringen om sannsynlighet. Det kan bare variere mellom 0 og 1. Hvis sannsynligheten for en hendelse er 0, er det umulig at det kommer til å skje. På den annen side, hvis sannsynligheten er 1, så skjer det helt sikkert.